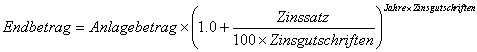 |
|
|
|||||||||||||||||
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Zinsen und ZinseszinsenDas Wichtigste bei jeder Geldanlage sind die Zinsen. Ziel eines jeden Kapitalanlegers ist es, dass das eingesetzte Kapital möglichst hoch verzinst wird. Eigentlich gibt es zum Thema Zinsen nicht viel zu sagen; aber es gibt doch einige Fragen zum Thema Zinsen, die so manchem semiprofessionellen Kapitalanleger noch ein Krübeln hervorrufen, als da wären zum Beispiel:
Wenn dir Fragen wie diese alle klar sind, dann brauchst du nicht weiterlesen. Auf diese und ähnliche Fragen gehe ich im Folgenden genauer ein. Berechnung der ZinsenWer sein Geld auf einem Tagesgeldkonto gut verzinst anlegt oder das Glück hat, auf seinem Girokonto Guthabenzinsen zu bekommen, der erhält von seiner Bank eine monatliche, vierteljährliche oder jährliche tagesgenaue Zinsgutschrift. Was bedeuten diese Begriffe im Einzelnen? Ich erkläre die Begriffe anhand von Beispielen. Beispiel 1: Tagesgeldkonto mit folgenden Konditionen:
Du hast also ein Tagesgeldkonto, welches dein angelegtes Kapital mit 6% pro Jahr verzinst. Es ist einleuchtend, dass du, wenn du am 01. Januar eines Jahres 10.000 € anlegst, am Jahresende eine Zinsgutschrift in Höhe von 600 € bekommst, also nach exakt einem Jahr 10.600 € auf deinem Konto hast. Die 6% p.a. bekommst du auch, wenn du das Geld nur für einen Teilzeitraum eines Jahres anlegst. Legst du zum Beispiel 10.000 € vom 01. Januar bis zum 30. Juni eines Jahres an, so erhälst du 300 € Zinsen, jedoch nicht am 30. Juni sondern am 31. Dezember, da die Zinsen ja nur einmal pro Jahr gutgeschrieben werden. Eine tagesgenaue Zinsberechnung bedeutet, dass du auf dein angelegtes Kapital die versprochene jährliche Verzinsung reduziert auf die Anzahl der Tage bekommst. Nehmen wir an, du legst 10.000 € vom 05. Mai bis zum 25. Mai, also für 20 Tage an. Dann berechnet die Bank deine Zinsen wie folgt: 6% Zinsen auf 10.000 € ergäben 600 € pro Jahr. Da du das Geld nur an 20 von 365 Tagen angelegt hast, ergeben sich deine Zinsen gemäß: 600€ x 20 / 365 = 33€. Wie berechnet nun eine Bank deine jährlichen Zinsen, wenn du alle paar Tage Geld einzahlst oder abhebst? Die tagesgenaue Berechnung erfolgt nach obigem Prinzip für jeden einzelnen Tag des Jahres. Die Bank, d.h. deren Computer, überprüft dein Guthaben in jeder Nacht, multipliziert dieses mit dem aktuellen Zinssatz und teilt das Ergebnis durch 365 Tage, d.h. du bekommst jeden Tag ein kleines Stückchen Zinsen, was aber nicht heißt, dass du über dieses am anderen Tag auch verfügen kannst, denn Zinsberechnung und Zinsgutschrift sind zwei verschiedene Paar Stiefel bzw. finden an zwei unterschiedlichen Tagen statt. Beispiel 2: Tagesgeldkonto mit folgenden Konditionen:
Bei diesem Tagesgeldkonto erhälst du gleich viel Zinsen wie bei dem vorigen, jedoch werden dir die Zinsen nicht am Ende vom Jahr sondern jeweils am Quartalsende gutgeschrieben. Bei einer Anlage von 10.000 € vom 01. Januar bis zum 31. Dezember erhälst du also nicht am Ende einmalig 600 € Zinsen, sondern 4 mal ca. 150 €, jeweils am Quartalsende. Die folgende Tabelle zeigt, wie sich die 10.000 € im Laufe des Jahres weiterentwickeln. Der jeweilige Quartalszins berechnet sich wie folgt (Beispiel 1. Quartal):
Anhand dieses Beispieles wird deutlich, wie sich der Zinseszins-Effekt auf das anfängliche Guthaben von 10.000 € auswirkt. Während man bei einer jährlichen Zinsgutschrift am Jahresende 600 € mehr auf seinem Konto hat, findet man bei einer quartalsweisen Zinsgutschrift bei gleichem Zinssatz am Jahresende 613,64 € Euro mehr auf seinem Konto. Bei einer quartalsweisen Verzinsung von 6% pro Jahr macht sich also der Zinseszins-Effekt insofern bemerkbar, dass man am Jahresende 6,14% mehr Kapital auf seinem Konto hat. Damit sind wir bereits mitten in der Zinseszins-Berechnung. Dieses Thema behandeln wir ausführlich im nächsten Kapitel. Zinseszins-BerechnungIm vorigen Kapitel haben wir gesehen, wie aus 10.000 € bei einer jährlichen Verzinsung von 6% anstatt 10.600 € plötzlich 10.614 € werden, wenn die Zinsen nicht am Jahresende sondern jeweils am Quartalsende ausbezahlt werden. Den Differenzbetrag von 14 € bezeichnen die Banken gerne als Zinseszins, also die Zinserträge auf die Zinsen. Im Folgenden nehmen wir das Thema Zinseszins etwas genauer unter die Lupe. Wir beginnen mit einem ganz einfachen Beispiel, wie man es oft bei langfristigen Angeboten bei Banken findet. Beispiel 3: Kapitalverdopplung in 10 Jahren
Die Bank verspricht dir also, dass bei einem jährlichen Zinssatz von 7% aus deinen 10.000 € nach 10 Jahren 20.000 € werden. Hat sie recht? Bei 7% Zinsen pro Jahr, 10 Jahre lang, kommt man doch nur auf ca. 70% Kapitalzuwachs, oder? Machen wir die Rechnung mit Berücksichtigung der Zinseszinsen.
Wir sehen, die Bank hat im Prinzip recht, dass sich nach 10 Jahren dein Kapital in Folge des Zinseszins-Effektes quasi verdoppelt hat. Mathematiker und Leute, die vor einer mathematischen Mit dieser Formel kann man für jeden beliebigen Anlagebetrag und jeden beliebigen Zinssatz (natürlich auch Zinssätze wie 4.25%) ausrechnen, was mit dem eingesetzten Kapital nach einer beliebigen Anzahl von Jahren (auch z.B. 3.5 Jahre möglich) wird.
Bitte erinnere dich, dass wir für dieses Beispiel 3 angenommen haben, dass die Zinsen jährlich gutgeschrieben werden. Ist dies nicht der Fall, so müssen obige Formeln noch zum einen zusätzlichen Faktor ergänzt werden. Dies machen wir anhand unseres obigen Beispieles 2: Beispiel 4: Tagesgeldkonto mit folgenden Konditionen:
Jetzt geht's ins Eingemachte: Wir berechnen den Zuwachs unseres eingesetzen Kapitals, falls die Zinsen quartalsweise gutgeschrieben werden. Eine quartalsweise Zinsauszahlung bedeutet, dass man 4 Zinsgutschriften pro Jahr bekommt. Werden die Zinsen monatlich gutgeschrieben, erhält man 12 Zinsgutschriften pro Jahr. Unsere Formel vom vorigen Beispiel wird um diese Anzahl der Zinsgutschriften erweitert:
Testen wir diese Formel, indem wir den Endbetrag von 10.613.64 € in der Tabelle aus Beispiel 2 nachrechnen. Wir setzen also in unsere neue Formel Anlagebetrag=10.000, Zinssatz=6, Zinsgutschriften=4, Jahre=1 ein und berechnen: Mit dieser Formel können wir auch nachrechnen, was aus dem eingesetzten Kapital nach einem Quartal wird, indem wir für die Anzahl der Jahre 1/4=0.25 einsetzen. Beispiel 5: Tagesgeldkonto mit folgenden Konditionen:
In Beispiel 2 und Beispiel 4 haben wir ausgerechnet, dass man aus 10.000 € bei einer jährlichen Verzinsung von 6% knapp 14 € mehr macht, wenn die Zinsen quartalsweise ausbezahlt werden. Rechnen wir abschließend mit obiger Formel noch aus, wieviel man nach einem Jahr erhält, wenn die Zinsen monatlich ausgezahlt werden. Wir setzen also ein für Anlagebetrag=10.000, Zinssatz=6, Zinsgutschriften=12, Jahre=1 und erhalten: Wir sehen, dass gegenüber einer jährlichen Zinsauszahlung 16,78 € mehr herauskommen, gegenüber einer quartalsweisen Zinsauszahlung jedoch nur 3,14 € mehr rausspringen. Rechnen wir abschließend noch aus, was aus unserem Kapital werden würde, wenn wir täglich eine Zinsgutschrift erhalten würden (nicht zu verwechseln mit einer tagesgenauen Zinsberechnung): Wir setzen also ein für Anlagebetrag=10.000, Zinssatz=6, Zinsgutschriften=365, Jahre=1 und erhalten: Es gibt gegenüber der monatlichen Zinsauszahlung also nochmals 1,53 € mehr. Copyright: Patrick Wagner, www.patrickwagner.de |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|
Formel nicht zurückschrecken, können obige iterative Tabellenrechnung mit einem Taschenrechner schnell durchführen. Setzt man in die Formel für Anlagebetrag die Zahl 10.000, für Zinssatz die Zahl 7 und für Jahre die Zahl 10 ein, so erhält man das Ergebnis aus der Tabelle: 19.672 = 10.000 x (1 + 7/100)^10
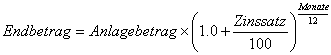Wer über kleinere Zeiträume denkt, kann dieselbe Formel anwenden um die Weiterentwicklung seines Anlagebetrages über einen gewissen Zeitraum zu berechnen. Für die Anzahl der Jahre gibt man dann entsprechende Bruchteile eines Jahres ein. Wer z.B. wissen möchte, wie sich sein Kapital nach 3 Monaten vergrößert, setzt für die Anzahl der Jahre 3/12 = 0.25 ein.
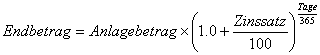Selbstverständlich kann man auf den Tag genau rechnen, indem man z.B. bei 20 Tagen für die Anzahl der Jahre 20/365 einsetzt.
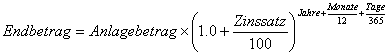Und natürlich lassen sich auch Jahre, Monate und Tage kombinieren, indem man in den Exponenten die Anzahl der Jahre plus die durch 12 geteilte Anzahl von Monaten plus die durch 365 geteilte Anzahl von Tagen einsetzt.